
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Funktionen - Grundfunktionen

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Komplexe Analysis - Komplexe Funktionen - Grundfunktionen | |
Komplexe Funktion |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Für den
Real- und Imaginärteil von ![]() gilt
gilt
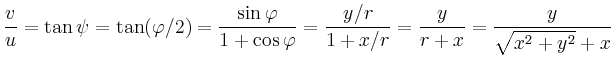



![$\displaystyle \operatorname{arg}(\sqrt{z})\in\left(-\frac{\pi}{2},\frac{\pi}{2}\right]\,.$](/inhalt/beispiel/beispiel1028/img15.png)
Bei der Definition der Wurzelfunktion ist zu beachten, dass
bei einer konsistenten Wahl des Vorzeichens (z.B. für den
Hauptzweig) der Grenzwert bei Annäherung an die negative reelle
Achse von oben sich von dem Grenzwert bei Annäherung von unten unterscheidet. Das
Definitionsgebiet ![]() sollte also keine geschlossene Kurve um den
Ursprung enthalten. Beispielsweise kann der Sektor
sollte also keine geschlossene Kurve um den
Ursprung enthalten. Beispielsweise kann der Sektor
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 21.11.2013 |