Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Gruppentheorie - Abelsche Gruppen - Freie abelsche Gruppen

Rang einer freien abelschen Gruppe

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Sei $ A$ eine freie abelsche Gruppe mit Basis $ B$. Es sei $ \vert B\vert=n$. Ist $ C$ eine andere Basis von $ A$, dann gilt

$\displaystyle \vert C\vert=\vert B\vert=n. $

Man nennt $ n$ den Rang von $ A$.
Ist $ U$ eine Untergruppe von $ A$, dann ist $ U$ frei und vom Rang $ \leq n$.
(Autoren: Kimmerle/Höfert)
Seien $ B$ und $ C$ Basen von $ A$. Für eine endliche Menge $ X$ mit $ \vert X\vert=n$ definiert

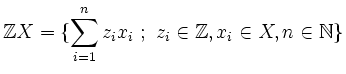
$\displaystyle {\mathbb{Z}}X = \{\sum \limits_{i=1}^n z_ix_i \ ; \ z_i \in {\mathbb{Z}} , x_i \in X , n \in {\mathbb{N}}\} $

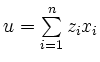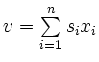die Menge der formalen $ {\mathbb{Z}}-$Linearkombinationen aus $ X$. Für zwei Elemente $ u,v \in {\mathbb{Z}}X$ mit $ u=\sum \limits_{i=1}^n z_ix_i$ und $ v=\sum \limits_{i=1}^n s_ix_i$ definiert man durch

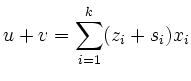
$\displaystyle u+v=\sum \limits_{i=1}^k (z_i+s_i)x_i $

eine Addition. Mit dieser Addition wird $ {\mathbb{Z}}X$ zu einer abelschen Gruppe, die per Konstruktion $ X$ als Basis besitzt.

Analog wird $ {\mathbb{Q}}X$ definiert und zu einem $ {\mathbb{Q}}-$Vektorraum mit Basis $ X$, wenn für $ u \in {\mathbb{Q}}X$ und $ q \in {\mathbb{Q}}$ in die skalare Multiplikation als

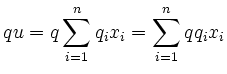
$\displaystyle qu=q \sum \limits_{i=1}^nq_ix_i= \sum \limits_{i=1}^nqq_ix_i $

definiert ist. Es gilt $ {\mathbb{Z}}X \subset {\mathbb{Q}}X$.

Ist nun $ A$ eine freie abelsche Gruppe mit Basis $ B$, dann ist $ A\cong {\mathbb{Z}}B$ (via $ b \mapsto b$).

Sind $ B$ und $ C$ Basen von $ A$, dann gilt $ {\mathbb{Z}}B \cong A \cong {\mathbb{Z}}C$, und damit $ V:= {\mathbb{Q}}B \cong {\mathbb{Q}}C$, wobei $ B$ und $ C$ Basen von $ V$ sind. Da verschiedene Basen eines Vektorraums gleiche Kardinalität besitzen gilt $ \vert B\vert=\vert C\vert$.

Sei nun $ U \leq A$. Für $ A=0$ ist die letzte Aussage offensichtlich richtig. Sei also $ A\neq 0$, $ B= \{b_1, \ldots b_n\}$ eine $ {\mathbb{Z}}-$Basis von $ A$. Falls $ U \leq \langle b_1 , \ldots , b_{n-1} \rangle$ ist, dann folgt die Aussage via Induktion. Man kann also annehmen, dass ein Element $ u\in U$ existiert mit $ u=z_1b_1+ \ldots + z_n b_n$ mit $ z_n \neq 0$.

Behauptung 1: $ V=\{z \in {\mathbb{Z}} ; z=z_n \textrm{ für ein } u \in U\} \leq {\mathbb{Z}}$.

Beweis: Seien $ s,t \in V$, dann existieren $ u,v \in U$ mit $ u=s_1b_1 + \ldots + s b_n$ und $ v=t_1b_1 + \ldots + t b_n$. Dann ist auch $ u-v \in U$, da $ U \leq A$, und es gilt $ u-v=(s_1-t_1)b_1 + \ldots + (s-t)b_n$. Damit ist auch $ s-t \in V$ und das Untergruppenkriterium liefert die Behauptung.

Behauptung 2: $ V = \tilde{n}\mathbb{Z}$ mit $ \tilde{n} \in \mathbb{N}$.

Beweis: Die Behauptung folgt mit dem Euklidischen Algorithmus. Man beachte, dass $ z_n \neq 0$ ist, und damit $ \tilde{n} \neq 0$ gilt.

Setzt man $ U_{n-1}=U \cap \langle b_1 , \ldots , b_{n-1} \rangle$, dann besitzt $ U_{n-1}$ via Induktion eine Basis $ w_1 , \ldots , w_m$ mit $ m \leq n-1$. Nach Behauptung 1 und 2 gibt es ein $ \tilde{u} \in V$ mit $ \tilde{u}=z_1b_1 + \ldots + z_nb_n$ und $ z_n=\tilde{n}$.

Behauptung 3: $ \{w_1, \ldots , w_m ,\tilde{u}\}$ ist eine $ {\mathbb{Z}}-$Basis von $ U$.

Beweis: Man sieht leicht, dass $ \{w_1, \ldots , w_m ,\tilde{u}\}$ linear unabhängig und eine Teilmenge von $ U$ ist. Es genügt also zu zeigen, dass die Menge eine Erzeugendensystem ist.

Sei $ u\in U$ gegeben, dann ist $ u=s_1b_1 + \ldots + s_nb_n$, $ s_i \in {\mathbb{Z}}$. Nach Behauptung 2 gilt $ s_n=z \tilde{n}$, $ z \in {\mathbb{Z}}$. Bildet man $ u-z\tilde{u}$, dann wird der Koeffizient von $ b_n$ zu Null, und es gilt $ u-z \tilde{u} \in \langle b_1, \ldots , b_{n-1} \rangle$. Also ist $ u-z\tilde{u} \in U \cap\langle b_1, \ldots , b_{n-1} \rangle =U_{n-1}$ und $ u-z\tilde{u}$ ist eine Linearkombination der $ w_1 , \ldots , w_m$. Damit ist $ u$ eine Linearkombination der $ w_1, \ldots , w_m, \tilde{u}$ und Behauptung 3 ist gezeigt.

Da $ m \leq n-1$ ist, hat $ \{w_1, \ldots , w_m ,\tilde{u}\}$ höchstens $ n$ Elemente.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.11.2008