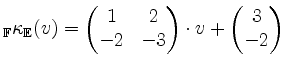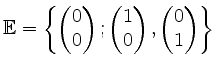 und
und
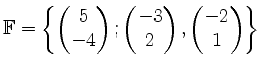 .
.
Um die Trafo von
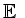 nach
nach
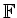 zu bestimmen betrachte:
zu bestimmen betrachte:
Analoges gilt für den zweiten und den Translationsvektor. Da die Koeffizienten der Linearkombination in den Spalten eingetragen werden, erhält man somit:
Um an die umgekehrte Koordinatentransformation zu gelangen, betrachte:
Die Koeffizienten 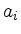 stehen wie beim Vorherigen in der ersten Spalte. Berechne nun die zweite Spalte:
Damit ergibt sich die Trafomatrix
stehen wie beim Vorherigen in der ersten Spalte. Berechne nun die zweite Spalte:
Damit ergibt sich die Trafomatrix
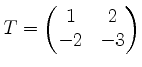 .
Erhalte nun die passende Translation:
Da die Translation rückgängig gemacht werden muss, gilt für den Translationsvektor also
.
Erhalte nun die passende Translation:
Da die Translation rückgängig gemacht werden muss, gilt für den Translationsvektor also
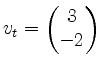 und somit
insgesamt:
und somit
insgesamt:
| |
automatisch erstellt
am 14.7.2008 |


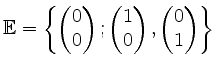 und
und
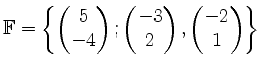 .
.
![]() nach
nach
![]() zu bestimmen betrachte:
zu bestimmen betrachte:
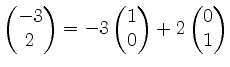
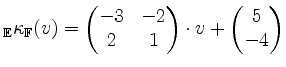
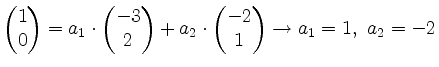
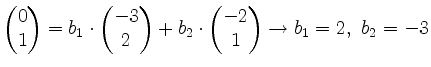
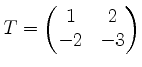 .
Erhalte nun die passende Translation:
.
Erhalte nun die passende Translation:
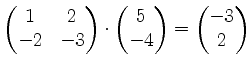
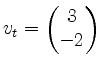 und somit
insgesamt:
und somit
insgesamt: