

Mathematik-Online-Kurs: Vorkurs Mathematik - Analysis - Extremwerte und Kurvendiskussion

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Kurs: Vorkurs Mathematik - Analysis - Extremwerte und Kurvendiskussion | ||
Asymptoten rationaler Funktionen | ||
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
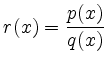
hat genau dann eine lineare Asymptote, wenn Grad
Für
Grad ![]() Grad
Grad ![]() gilt
gilt
d.h. die
![\includegraphics[width=0.4\moimageheight]{asymptoten1.eps}](/inhalt/beispiel/beispiel44/img8.png)
![\includegraphics[width=0.4\moimageheight]{asymptoten2.eps}](/inhalt/beispiel/beispiel44/img9.png)
![\includegraphics[width=0.4\moimageheight]{asymptoten3.eps}](/inhalt/beispiel/beispiel44/img10.png)
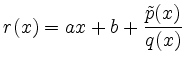
mit Grad
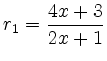 und
und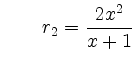
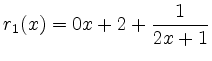 und
und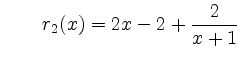
![\includegraphics[width=7.4cm]{bsp_asymptote1_1.eps}](/inhalt/beispiel/beispiel1236/img7.png)
![\includegraphics[width=7.4cm]{bsp_asymptote2_1.eps}](/inhalt/beispiel/beispiel1236/img8.png)
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 23.10.2009 |