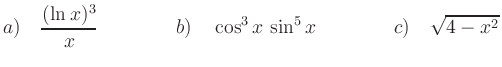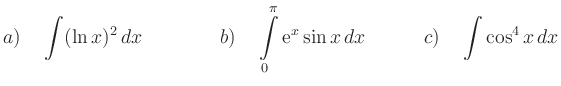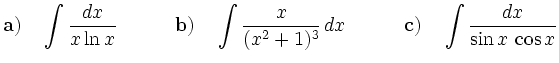Schon kurz nach Studienbeginn ist Freshman Felix überzeugt,
zur Lösung der HM-Aufgaben einen High-End PC zu benötigen.
Kosten: 5000 DM - Sparbuchstand: 0 DM.
- a)
- Seine Bank bietet ihm einen Kredit, der durch
 gleich
große Monatsraten getilgt werden soll.
Die Restschuld wird monatlich mit
gleich
große Monatsraten getilgt werden soll.
Die Restschuld wird monatlich mit 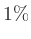 verzinst;
die erste Rate wird einen Monat nach Kreditaufnahme bezahlt.
Wie hoch sind die Monatsraten
verzinst;
die erste Rate wird einen Monat nach Kreditaufnahme bezahlt.
Wie hoch sind die Monatsraten 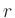 anzusetzen?
anzusetzen?
- b)
- Felix entschließt sich, den Kredit ohne Ratenzahlungen nach
zwei Jahren zurückzubezahlen. Wie hoch ist diese Summe bei
jährlicher, vierteljährlicher, monatlicher, täglicher
oder stetiger Verzinsung mit
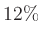 bzw.
bzw. 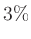 bzw.
bzw. 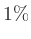 ...?
Bestimmen Sie jeweils den jährlichen Effektivzins.
...?
Bestimmen Sie jeweils den jährlichen Effektivzins.
Die Funktion 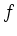 sei an einer Stelle
sei an einer Stelle
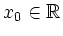 differenzierbar und
genüge für alle
differenzierbar und
genüge für alle
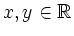 der Gleichung
der Gleichung
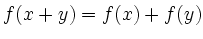 .
.
- a)
- Zeigen Sie mit Hilfe des Differenzenquotienten, dass
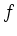 auf ganz
auf ganz
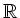 differenzierbar ist.
differenzierbar ist.
- b)
- Beweisen Sie, dass eine Konstante
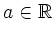 existiert mit
existiert mit
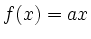 für alle
für alle
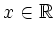 .
.
(Autor: Joachim Wipper)
Ein Geländeprofil wird näherungsweise durch die Funktion
beschrieben. Die beiden Berge sollen durch eine Seilbahn verbunden werden, die
an beiden Enden tangential zur obigen Profilkurve verläuft
(vgl.Abbildung).
Wo müssen die beiden Stationen 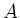 und
und 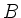 gebaut werden - und welche
Länge hat die Seilbahnstrecke? Der Durchhang des Seils ist zu
vernachlässigen.
gebaut werden - und welche
Länge hat die Seilbahnstrecke? Der Durchhang des Seils ist zu
vernachlässigen.
(Autor: Apprich)
Differenzieren Sie:
Gegeben sei die Funktion
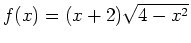 .
.
- a)
- Für welche
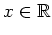 ist
ist 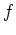 definiert? Untersuchen
Sie, wo
definiert? Untersuchen
Sie, wo 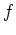 differenzierbar ist, und berechnen Sie
differenzierbar ist, und berechnen Sie 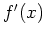 .
.
- b)
- Welche Nullstellen und lokalen Extrema besitzt
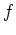 ?
?
- c)
- Wie verhält sich
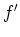 am Rand des Definitionsbereichs?
am Rand des Definitionsbereichs?
- d)
- Skizzieren Sie den Graph von
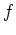 .
.
(Aus: Kimmerle/Roggenkamp/Rump, SS 1998)
Für
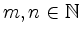 sei
sei 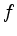
- a)
- Untersuchen Sie
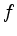 auf Nullstellen und lokale Extrema.
Wie verhält sich
auf Nullstellen und lokale Extrema.
Wie verhält sich 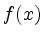 für
für
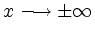 ?
?
- b)
- Skizzieren Sie den Graph von
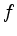 im Fall
im Fall 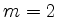 und
und 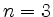 .
.
- c)
- Berechnen Sie den Inhalt der Fläche, die der Graph von
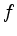 mit der
mit der 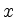 -Achse einschließt.
-Achse einschließt.
Seien 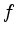 und
und 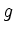 die durch
die durch
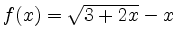 und
und
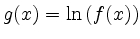 gegebenen reellwertigen Funktionen.
gegebenen reellwertigen Funktionen.
- a)
- Bestimmen Sie den Definitionsbereich von
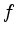 und skizzieren
Sie den Graph. Wür welche
und skizzieren
Sie den Graph. Wür welche 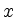 ist die Funktion
ist die Funktion 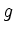 definiert?
definiert?
- b)
- Untersuchen Sie
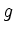 auf Nullstellen, Asymptoten und lokale
Extrema.
auf Nullstellen, Asymptoten und lokale
Extrema.
- c)
- Wie verhalten sich
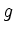 und
und 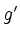 an den Randpunkten des
Definitionsbereichs?
an den Randpunkten des
Definitionsbereichs?
- d)
- Zeichnen Sie den Graph der Funktion
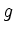 .
.
Hinweis:
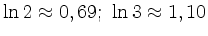 .
.
(Aus: Kimmerle/Roggenkamp/Rump, SS 1998)
Die Vorderfront eines Gewächshauses soll die Form eines achsensymmetrischen Fünfecks mit drei rechten Winkeln besitzen
(vgl.Abbildung). Der Umfang darf maximal 20m betragen.
Wie ist die Breite 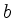 und Höhe
und Höhe 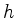 der Seitenwand zu wählen, damit
die Fläche
der Seitenwand zu wählen, damit
die Fläche 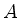 der Vorderfront maximal wird?
der Vorderfront maximal wird?
(Autor: Apprich)
Welchen Weg muß ein Mensch im Punkt 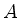 einschlagen, um möglichst schnell zu der
Insel
einschlagen, um möglichst schnell zu der
Insel 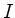 zu gelangen, wenn er fünfmal so schnell läuft, wie er zu
schwimmen vermag?
zu gelangen, wenn er fünfmal so schnell läuft, wie er zu
schwimmen vermag?
Bilden Sie Stammfunktionen von
(Autor: Klaus Höllig)
Bestimmen Sie die folgenden Integrale mit Hilfe partieller Integration.
(Autor: Klaus Höllig)
Bestimmen Sie die folgenden Integrale durch geeignete Substitutionen:
(Aus: Kimmerle/Roggenkamp/Rump, SS 1998)
| |
automatisch erstellt
am 23.10.2009 |




![$\displaystyle f(x)=\left\{\begin{array}{lcl} -\frac{1}{15}\,x^2+\frac{1}{5}\,x ...
...frac{2}{5}\,x-\frac{3}{5}, & {\mbox{f\uml ur}} & x\in (3,6]
\end{array}\right. $](/inhalt/aufgabe/aufgabe111/img1.png)
![\includegraphics[width=11cm]{g16_bild1}](/inhalt/aufgabe/aufgabe111/img2.png)
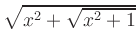
![]() und Höhe
und Höhe ![]() der Seitenwand zu wählen, damit
die Fläche
der Seitenwand zu wählen, damit
die Fläche ![]() der Vorderfront maximal wird?
der Vorderfront maximal wird?
![\includegraphics[width=3.5cm]{g25_bild1}](/inhalt/aufgabe/aufgabe120/img4.png)
![\includegraphics[width=.7\linewidth]{A775_2_bild.eps}](/inhalt/aufgabe/aufgabe393/img3.png)