Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Vektorräume

Lineare Unabhängigkeit

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Vektoren $ v_1,\dots,v_m$ heißen linear abhängig, wenn es Skalare $ \alpha_1,\dots,\alpha_m$ gibt mit

$\displaystyle \alpha_1 v_1 + \dots + \alpha_m v_m = 0 $

und mindestens einem $ \alpha_i \neq 0$. Andernfalls heißen sie linear unabhängig.

Allgemeiner bezeichnet man eine Menge $ M$ von Vektoren als linear unabhängig, wenn jede endliche Teilmenge von $ M$ aus linear unabhängigen Vektoren besteht. Andernfalls heißt $ M$ linear abhängig.

Man beachte, dass im Sinne der linearen Algebra zwar unendliche Mengen $ M$ zugelassen sind, aber nur endliche Linearkombinationen. So ist z. B. im Vektorraum der Folgen die Menge

$\displaystyle e=(1,1,\ldots)^{\operatorname t},\, e_1=(1,0,0,\ldots)^{\operatorname t},\, e_2=(0,1,0,\ldots)^{\operatorname t},\, \ldots $

linear unabhängig, obwohl

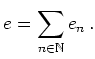
$\displaystyle e = \sum_{n\in\mathbb{N}}e_n\, . $

Es gibt keine endliche Darstellung der konstanten Folge $ e$ mit den kanonischen Einheitsvektoren.

(Autoren: App/Höllig)
Zwei Vektoren im $ \mathbb{R}^2$ sind genau dann linear unabhängig, wenn keiner der beiden ein Vielfaches des anderen ist. So sind z. B. die Vektoren $ (1,0)^{\operatorname t}$ und $ (1,1)^{\operatorname t}$ linear unabhängig, denn der Ansatz

$\displaystyle \alpha(1,0)^{\operatorname t}+$ $\displaystyle \beta(1,1)^{\operatorname t}= (0,0)^{\operatorname t}$    

liefert


$\displaystyle \beta =$ $\displaystyle \alpha =0\,.$    

Hingegen sind die Vektoren $ (0,0)^{\operatorname t}$ und $ (2,3)^{\operatorname t}$ linear abhängig, denn

$\displaystyle (0,0)^{\operatorname t}=$ $\displaystyle 0(2,3)^{\operatorname t}$    

bzw.


$\displaystyle 1(0,0)^{\operatorname t}+$ $\displaystyle 0(2,3)^{\operatorname t}= (0,0)^{\operatorname t}\, ;$    

es existiert also eine nichttriviale Darstellung des Nullvektors.

Drei Vektoren $ u,v,w$ im $ \mathbb{R}^2$ sind immer linear abhängig, denn der Ansatz

$\displaystyle \alpha u +$ $\displaystyle \beta v + \gamma w = 0$    

führt auf ein unterbestimmtes, homogenes lineares Gleichungssystem


$\displaystyle \alpha u_1 +$ $\displaystyle \beta v_1 + \gamma w_1 = 0$    
$\displaystyle \alpha u_2 +$ $\displaystyle \beta v_2 + \gamma w_2 = 0$    

für $ \alpha, \beta, \gamma$, das immer eine nichttriviale Lösung besitzt.

(Autoren: App/Höllig)
Wie im Zweidimensionalen sind zwei Vektoren im $ \mathbb{R}^3$ linear abhängig, wenn sie parallel sind, d.h. wenn ein Vektor ein Vielfaches des anderen ist.

Drei Vektoren sind linear abhängig, wenn zwei Vektoren parallel sind oder wenn ein Vektor in der von den beiden anderen Vektoren aufgespannten Ebene liegt. Beispielsweise gilt für

$\displaystyle u = (1,2,-3)^{\operatorname t},\,v = (4,-6,2)^{\operatorname t},\,w = (-9,3,6)^{\operatorname t} $

$ 6u + 3v + 2w = (0,0,0)^{\operatorname t}$; die Vektoren sind also linear abhängig.

Definitionsgemäß ist der Test für lineare Abhängigkeit äquivalent zu einem homogenen linearen Gleichungssystem

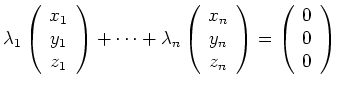
$\displaystyle \lambda_1 \left(\begin{array}{c} x_1 \\ y_1 \\ z_1 \end{arra... ...d{array}\right) = \left(\begin{array}{c} 0 \\ 0 \\ 0 \end{array}\right) $

für die Skalare $ \lambda_i$. Dies zeigt insbesondere, dass vier Vektoren im $ \mathbb{R}^3$ immer linear abhängig sind.
(Autoren: App/Höllig)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009