Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Vektoren

Spatprodukt

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Das Spatprodukt

$\displaystyle \bigl[\vec{a},\vec{b},\vec{c}\bigr] = \vec{a}\cdot(\vec{b}\times\vec{c}) = a_1(b_2c_3-b_3c_2)+a_2(b_3c_1-b_1c_3)+a_3(b_1c_2-b_2c_1)$    

stimmt bis auf Vorzeichen mit dem Volumen des von den drei Vektoren $ \vec{a}$ , $ \vec{b}$ , $ \vec{c}$ aufgespannten Spats überein. Es ist positiv, wenn die Vektoren $ \vec{a}$ , $ \vec{b}$ , $ \vec{c}$ gemäß der Rechten-Hand-Regel orientiert sind.
\includegraphics[width=7.4cm]{spatprodukt.eps}
Mit Hilfe des $ \varepsilon$ -Tensors lässt sich das Spatprodukt auch in der Form

$\displaystyle \bigl[\vec{a},\vec{b},\vec{c}\bigr]=\sum_{i,j,k=1}^3 \varepsilon_{i,j,k} a_i b_j c_k $

schreiben.

Als Beispiel wird das Spatprodukt der Vektoren

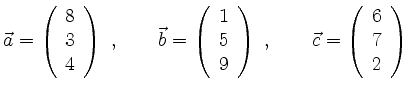
$\displaystyle \vec{a} = \left( \begin{array}{c} 8 \\ 3 \\ 4 \end{array} \right)... ...) \ , \qquad \vec{c} = \left( \begin{array}{c} 6 \\ 7 \\ 2 \end{array} \right) $

berechnet. Zunächst bildet man dazu das Kreuzprodukt

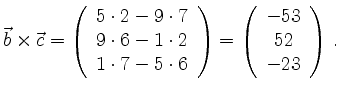
$\displaystyle \vec{b} \times \vec{c} = \left( \begin{array}{c} 5 \cdot 2 - 9 \c... ...ay} \right) = \left( \begin{array}{c} -53 \\ 52 \\ -23 \end{array} \right) \,. $

Das Skalarprodukt mit $ \vec{a}$ liefert dann

$\displaystyle \left[ \vec{a}, \vec{b}, \vec{c} \right] = \left( \begin{array}{c... ...\cdot \left( \begin{array}{c} -53 \\ 52 \\ -23 \end{array} \right) = -360 \,. $

(Autoren: Höllig/Kreitz)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009