

Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Komplexe Zahlen

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Komplexe Zahlen | ||
Eigenschaften des Betrags komplexer Zahlen | ||
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Der Betrag einer komplexen Zahl
![]() ist als
ist als
Die Positivität der Betragsfunktion ist offensichtlich und die Multiplikativität läßt sich mit Hilfe der Definition leicht nachrechnen.
Zum Beweis der Dreiecksungleichung quadriert man
die Ungleichungskette und erhält nach Subtraktion
von
![]()
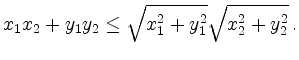
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 23.10.2009 |