

Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Komplexe Zahlen

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Komplexe Zahlen | ||
Multiplikation komplexer Zahlen | ||
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
![\includegraphics[width=.5\linewidth]{a_multiplikation_bild}](/inhalt/aussage/aussage379/img4.png)
Geometrisch entspricht die Multiplikation mit
einer komplexen Zahl
![]() einer Streckung um den Faktor
einer Streckung um den Faktor ![]() und einer
Drehung um den Winkel
und einer
Drehung um den Winkel ![]() .
.
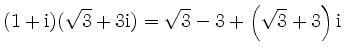
Für
Wie die Beispiele zeigen, ist die Multiplikation in Polarform im allgemeinen einfacher. Dies trifft insbesondere für die Bildung von Potenzen zu.
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 23.10.2009 |