
Mathematik-Online-Kurs: Repetitorium HM I - Folgen, Reihen, stetige Funktionen

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Repetitorium HM I - Folgen, Reihen, stetige Funktionen | |
Funktionen |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Funktionen allgemein.
Seien
![]() und
und
![]() zwei Mengen. Eine Funktion (auch Abbildung genannt) ist eine Vorschrift
zwei Mengen. Eine Funktion (auch Abbildung genannt) ist eine Vorschrift
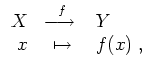
Sei das cartesische Produkt
![]() von
von
![]() und
und
![]() definiert als
definiert als
Formal kann man Funktionen auch über den Graphen
![]() von
von
![]() einführen - ein Funktionsgraph ist eine Teilmenge
einführen - ein Funktionsgraph ist eine Teilmenge
![]() von
von
![]() derart, daß für jedes
derart, daß für jedes
![]() genau
ein
genau
ein
![]() mit
mit
![]() existiert.
existiert.
Sei
![]() , und seien
, und seien
![]() und
und
![]() Teilmengen.
Wir definieren das Bild
Teilmengen.
Wir definieren das Bild
![]() und das Urbild
und das Urbild
![]() via
via
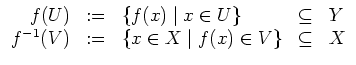
Ist
![]() eine Menge, so bezeichnen wir die Anzahl ihrer Elemente mit
eine Menge, so bezeichnen wir die Anzahl ihrer Elemente mit
![]() . Ist
. Ist
![]() eine unendliche Menge,
so schreiben wir
eine unendliche Menge,
so schreiben wir
![]() .
.
Die Funktion
![]() heißt injektiv, wenn
heißt injektiv, wenn
![]() für alle
für alle
![]() .
.
Die Funktion
![]() heißt surjektiv, wenn
heißt surjektiv, wenn
![]() für alle
für alle
![]() .
.
Die Funktion
![]() heißt bijektiv, wenn
heißt bijektiv, wenn
![]() für alle
für alle
![]() . Diesenfalls schreiben
wir auch
. Diesenfalls schreiben
wir auch
![]() für
für
![]() , und
, und
![]() definiert ebenfalls eine
bijektive Funktion, genannt die Umkehrabbildung zu
definiert ebenfalls eine
bijektive Funktion, genannt die Umkehrabbildung zu
![]() .
.
Vorsicht. Bezüglich jeder Funktion kann man Urbilder von Teilmengen nehmen. Es haben aber nur bijektive Funktionen eine Umkehrfunktion.
Kurz,
![]() ist injektiv, falls verschiedene Elemente auf verschiedene Bildelemente gehen.
Und
ist injektiv, falls verschiedene Elemente auf verschiedene Bildelemente gehen.
Und
![]() ist surjektiv, falls
ist surjektiv, falls
![]() .
.
Seien
![]() und
und
![]() Funktionen. Wir definieren die Verkettung
Funktionen. Wir definieren die Verkettung
![]() (gesprochen «
(gesprochen «
![]() nach
nach
![]() ») als
») als
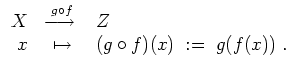
Ist
![]() bijektiv, so ist
bijektiv, so ist
![]() und
und
![]() , wobei
, wobei
![]() die identische Abbildung auf
die identische Abbildung auf
![]() bezeichnet.
bezeichnet.
Sind sowohl
![]() und
und
![]() bijektiv, so ist auch die Verkettung
bijektiv, so ist auch die Verkettung
![]() bijektiv, und es gilt
bijektiv, und es gilt
Reelle Funktionen (eindimensional).
Ist
![]() und
und
![]() , so sprechen wir von einer (eindimensionalen) reellen Funktion
, so sprechen wir von einer (eindimensionalen) reellen Funktion
![]() .
.
Es sei
![]() eine Funktion mit Definitionsbereich
eine Funktion mit Definitionsbereich
![]() .
.
![]() heißt monoton wachsend (bzw. monoton fallend),
falls für
heißt monoton wachsend (bzw. monoton fallend),
falls für
![]() mit
mit
![]() stets
stets
![]() (bzw.
(bzw.
![]() ) gilt.
) gilt.
![]() heißt streng monoton wachsend (bzw. streng monoton fallend), falls für
heißt streng monoton wachsend (bzw. streng monoton fallend), falls für
![]() mit
mit
![]() stets
stets
![]() (bzw.
(bzw.
![]() ) gilt.
) gilt.
![]() heißt monoton, falls sie monoton wachsend oder monoton fallend ist.
heißt monoton, falls sie monoton wachsend oder monoton fallend ist.
![]() heißt streng monoton, falls sie streng monoton wachsend oder streng monoton fallend ist.
heißt streng monoton, falls sie streng monoton wachsend oder streng monoton fallend ist.
Die Funktion
![]() heißt nach oben beschränkt (bzw. nach unten beschränkt), falls es ein
heißt nach oben beschränkt (bzw. nach unten beschränkt), falls es ein
![]() gibt mit
gibt mit
![]() (bzw.
(bzw.
![]() ) für alle
) für alle
![]() . Sie heißt beschränkt, falls sie sowohl
nach oben als auch nach unten beschränkt ist.
. Sie heißt beschränkt, falls sie sowohl
nach oben als auch nach unten beschränkt ist.
Sind
![]() und
und
![]() reelle Funktionen mit demselben Definitionsbereich
reelle Funktionen mit demselben Definitionsbereich
![]() , so definieren wir
auch die folgenden Funktionen.
, so definieren wir
auch die folgenden Funktionen.
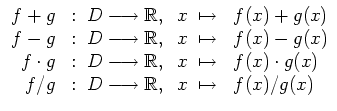
Für die Bildung von
![]() müssen wir natürlich voraussetzen, daß
müssen wir natürlich voraussetzen, daß
![]() für alle
für alle
![]() .
.
Seien
![]() ,
,
![]() . Als Definitionsbereich reeller Funktionen treten häufig Intervalle der
folgenden Form auf.
. Als Definitionsbereich reeller Funktionen treten häufig Intervalle der
folgenden Form auf.
![$ \mbox{$\displaystyle
\begin{array}{rcl}
{[a,b]} & := & \{ x\in\mathbb{R}\; \v...
...\
{(-\infty,b)} & := & \{ x\in\mathbb{R}\; \vert\; x < b\} \\
\end{array}$}$](/inhalt/aussage/aussage1154/img62.png)
Polynome und rationale Funktionen.
Ein (reelles) Polynom ist eine Funktion der Form
Ist
![]() , so heißt
, so heißt
![]() der Grad des Polynoms
der Grad des Polynoms
![]() . Sind alle Koeffizienten gleich
. Sind alle Koeffizienten gleich
![]() ,
so heißt
,
so heißt
![]() das Nullpolynom, geschrieben
das Nullpolynom, geschrieben
![]() , und man definiert
, und man definiert
![]() .
.
Sind
![]() und
und
![]() zwei Polynome, so können wir
zwei Polynome, so können wir
![]() durch
durch
![]() mit Rest teilen. Wir finden durch diese
Polynomdivision Polynome
mit Rest teilen. Wir finden durch diese
Polynomdivision Polynome
![]() und
und
![]() mit
mit
![]() und
und
Sind
![]() und
und
![]() zwei Polynome, so wird der Quotient
zwei Polynome, so wird der Quotient
![]() als rationale Funktion bezeichnet,
definiert auf
als rationale Funktion bezeichnet,
definiert auf
![]() .
.
Komplexe Funktionen, Fundamentalsatz der Algebra.
Analoge Begriffsbildungen gelten auch für komplexe Funktionen
![]() mit Definitionsbereich
mit Definitionsbereich
![]() ,
mit Ausnahme der Monotonie und der Intervalle. Eine solche Funktion heißt beschränkt genau dann, wenn für ein
,
mit Ausnahme der Monotonie und der Intervalle. Eine solche Funktion heißt beschränkt genau dann, wenn für ein
![]() stets
stets
![]() ist.
ist.
Komplexe Polynome
![]() haben nun die schöne Eigenschaft, laut Fundamentalsatz der
Algebra in ein Produkt von Linearfaktoren
haben nun die schöne Eigenschaft, laut Fundamentalsatz der
Algebra in ein Produkt von Linearfaktoren
Die Bestimmung der Nullstellen eines komplexen Polynoms kann ein verwickeltes Problem sein.
Folgen.
Ist
![]() für ein
für ein
![]() , so bezeichnet man eine Funktion
, so bezeichnet man eine Funktion
![]() als
(komplexwertige) Folge, und schreibt in der Regel
als
(komplexwertige) Folge, und schreibt in der Regel
![]() , sowie die gesamte Folge als
, sowie die gesamte Folge als
![]() . Geht
. Geht
![]() aus dem Kontext hervor, so schreibt man auch
aus dem Kontext hervor, so schreibt man auch
![]() .
Sind alle
.
Sind alle
![]() , so spricht man von einer reellwertigen Folge.
, so spricht man von einer reellwertigen Folge.
Eine reellwertige Folge heißt monoton wachsend, falls die zugehörige Funktion monoton wachsend ist, d.h. falls
![]() für alle
für alle
![]() . Analog monoton fallend usf.
. Analog monoton fallend usf.
| automatisch erstellt am 18.6.2004 |