
Mathematik-Online-Kurs: Prüfungsvorbereitung HM 1/2 SS08 - Lösungen zur Probeklausur 4

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Prüfungsvorbereitung HM 1/2 SS08 - Lösungen zur Probeklausur 4 | |
Aufgabe 3 |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Gebietseinteilungen:
![]()
Somit gilt erstmals für alle Tupel ![]() und
und ![]() , dass
, dass ![]() .
.
Sei nun ![]() und
und ![]() . Dann muss gelten:
. Dann muss gelten:
![]()
Damit ergeben sich die restlichen Tupel: ![]()
Somit erfüllen alle Punkte auf der ![]() -Achse, alle Punkte auf der
-Achse, alle Punkte auf der ![]() -Achse und alle Punkte auf der Parabel
-Achse und alle Punkte auf der Parabel ![]() die Gleichung
die Gleichung ![]()
![]()
![]()
![]()
Da ![]() folgt:
folgt:
![]()
![]()
![]()
Damit ergibt sich folgendes Schaubild:
![\includegraphics[width=8cm]{koordinatenkreuz-l-1}](/inhalt/loesung/loesung1136/img54.png)
Berechnung der kritischen Stellen
![]() :
:
![]() Berechne die Punkte
Berechne die Punkte ![]() mit
mit
![]() :
:
![]()
![]()
![$ [5x^2=3 \Leftrightarrow x_{1,2}=\pm \sqrt{\frac{3}{5}}\, \Rightarrow
y_{1,2} = 3\frac{3}{5}-3=-\frac{6}{5} ]$](/inhalt/loesung/loesung1136/img41.png)
![$ [\hookrightarrow \left(\sqrt{\frac{3}{5}},-\frac{6}{5}\right),\left(-\sqrt{\frac{3}{5}},-\frac{6}{5}\right)]$](/inhalt/loesung/loesung1136/img42.png) Berechne nun die Hessematrix, um damit die Extremwerte und Sattelpunkte zu bestimmen. Um die Art des Extremums zu erhalten, betrachte die Eigenwerte der Hessematrix.
Berechne nun die Hessematrix, um damit die Extremwerte und Sattelpunkte zu bestimmen. Um die Art des Extremums zu erhalten, betrachte die Eigenwerte der Hessematrix.
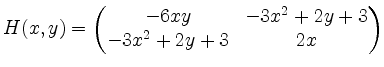
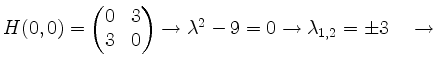 Sattelpunkt
Sattelpunkt
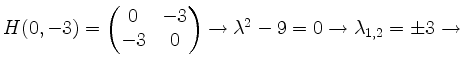 Sattelpunkt
Sattelpunkt
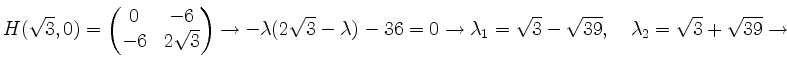 Sattelpunkt
Sattelpunkt
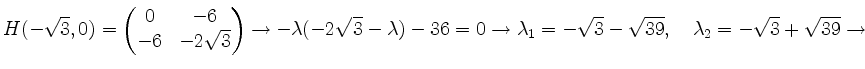 Sattelpunkt
Sattelpunkt
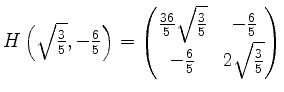
Für die Eigenwerte erhält man gerundet
![]() und
und
![]() und somit ist die Matrix positiv definit und es handelt sich um ein Minimum.
und somit ist die Matrix positiv definit und es handelt sich um ein Minimum.
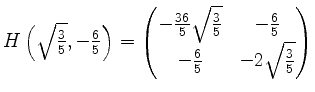
Für die Eigenwerte erhält man nun etwa
![]() und
und
![]()
Somit sind alle Eigenwerte negativ. Es liegt ein Maximum vor.
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 14.7.2008 |