Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Prüfungsvorbereitung HM 1/2 SS08 - Lösungen zur Probeklausur 3

Aufgabe 1

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
a)
Berechnen Sie den Konvergenzradius der folgenden Potenzreihe:
$ \sum \limits_{n=0}^{\infty} e^nx^n$
b)
Berechnen Sie den folgenden Grenzwert
$ \lim \limits_{x \rightarrow 0} \dfrac{\cos(2x)-\cos(x)}{x^2} = a$

Antwort:

a)
$ r=$ $ /e $
b)
$ a = $ /
(Brüche gekürzt mit positivem Nenner.)


  

[Andere Variante]
a)
Zu bestimmen ist der Konvergenzradius $ r$ der Potenzreihe:

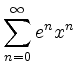
$\displaystyle \sum_{n=0}^{\infty}e^{n}x^{n} $

Die Anwendung des Wurzelkriteriums ergibt:

$\displaystyle r= \lim_{n\rightarrow \infty} \frac{1}{ \sup\sqrt[n]{e^n}}= \frac{1}{e} $

b)
Der folgende Grenzwert ist zu bestimmen:

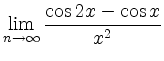
$\displaystyle \lim_{n\rightarrow \infty}\frac{\cos{2x}-\cos{x}}{x^2} $

Die Anwendung der Regel von L´Hospital ergibt mit $ f(x) = \cos{2x}-\cos{x}\rightarrow 0$ und $ g(x) = x^{2}\rightarrow 0$:

$\displaystyle \lim_{x\rightarrow 0}\frac{f(x)}{g(x)} = \lim_{x\rightarrow 0}\fr... ...}{0}\right] = \lim_{x\rightarrow 0}\frac{-4\cos{2x}+\cos{x}}{2} = -\frac{3}{2} $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.7.2008