Mathematik-Online-Kurs: Differentialrechnung - Übungen-Grenzwerte, Reihen und Stetigkeit -Konvergenz einer Reihe, Konvergenzradius einer Potenzreihe

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Differentialrechnung - Übungen - Grenzwerte, Reihen und Stetigkeit
	Konvergenz einer Reihe, Konvergenzradius einer Potenzreihe

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

Zeigen Sie die Konvergenz der Reihe

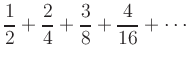
$\displaystyle \frac{1}{2} + \frac{2}{4} + \frac{3}{8} + \frac{4}{16} + \cdots$

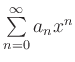und geben Sie eine Summendarstellung an. Gibt es eine Taylor-Reihe $\sum\limits_{n=0}^\infty a_n x^n$ , welche die Reihe als Spezialfall liefert, und welchen Konvergenzradius besitzt sie?

(Autor: Klaus Höllig)

[vorangehende Seite] [nachfolgende Seite]

[Gesamtverzeichnis][Seitenübersicht]

automatisch erstellt am 6.2.2018